Linear-feedback sum-capacity for Gaussian multiple access channels
Ehsan Ardestanizadeh, Michele Wigger, Young-Han Kim, and Tara Javidi
IEEE Transactions on Information Theory, vol. 58, no. 1, pp. 224–236, January 2012.
Preliminary results appeared in Proceedings of the IEEE International Symposium on Information Theory, pp. 430–434, Austin, Texas, June 2010.
The capacity region of the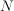 
-sender Gaussian multiple access channel
with feedback is not known in general. This paper studies the class of
linear-feedback codes that includes (nonlinear) nonfeedback codes at
one extreme and the linear-feedback codes by Schalkwijk and Kailath,
Ozarow, and Kramer at the other extreme. The linear-feedback
sum-capacity 
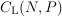under symmetric power constraints 
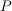is characterized, the maximum sum-rate achieved by linear-feedback
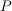codes when each sender has the equal block power constraint . In
particular, it is shown that Kramer's code achieves this
linear-feedback sum-capacity. The proof involves the dependence
balance condition introduced by Hekstra and Willems and extended by
Kramer and Gastpar, and the analysis of the resulting nonconvex
optimization problem via a Lagrange dual formulation. Finally, an
observation is presented based on the properties of the conditional
maximal correlation — an extension of the Hirschfeld-Gebelein-Renyi
maximal correlation — which reinforces the conjecture that Kramer's code
achieves not only the linear-feedback sum-capacity, but also the
sum-capacity itself (the maximum sum-rate achieved by arbitrary
feedback codes).