Channel capacity and state estimation for state-dependent Gaussian channels
Arak Sutivong, Mung Chiang, Thomas M. Cover, and Young-Han Kim
IEEE Transactions on Information Theory, vol. 51, no. 4, pp. 1486–1495, April 2005.
One-page abstract appeared in Proceedings of IEEE International Symposium on Information Theory, p. 226, Lausanne, Switzerland, June/July 2002.
We formulate a problem of state information transmission over a
state-dependent channel with states known at the transmitter. In
particular, we solve a problem of minimizing the mean-squared channel
state estimation error 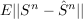 for a state-dependent
additive Gaussian channel
for a state-dependent
additive Gaussian channel 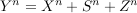 with an independent
and identically distributed (i.i.d.) Gaussian state sequence
with an independent
and identically distributed (i.i.d.) Gaussian state sequence 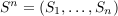 known at the transmitter and an unknown
i.i.d. additive Gaussian noise
known at the transmitter and an unknown
i.i.d. additive Gaussian noise 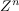 . We show that a simple technique
of direct state amplification (i.e.,
. We show that a simple technique
of direct state amplification (i.e., 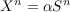 ), where the
transmitter uses its entire power budget to amplify the channel state,
yields the minimum mean-squared state estimation error. This same
channel can also be used to send additional independent information at
the expense of a higher channel state estimation error. We
characterize the optimal tradeoff between the rate R of the
independent information that can be reliably transmitted and the
mean-squared state estimation error D. We show that any optimal (R, D)
tradeoff pair can be achieved via a simple power-sharing technique,
whereby the transmitter power is appropriately allocated between pure
information transmission and state amplification.
), where the
transmitter uses its entire power budget to amplify the channel state,
yields the minimum mean-squared state estimation error. This same
channel can also be used to send additional independent information at
the expense of a higher channel state estimation error. We
characterize the optimal tradeoff between the rate R of the
independent information that can be reliably transmitted and the
mean-squared state estimation error D. We show that any optimal (R, D)
tradeoff pair can be achieved via a simple power-sharing technique,
whereby the transmitter power is appropriately allocated between pure
information transmission and state amplification.