Gaussian channel with noisy feedback and peak energy constraint
Yu Xiang and Young-Han Kim
IEEE Transactions on Information Theory, vol. 59, no. 8, pp. 4746–4756, August 2013.
Preliminary results appeared in Proceedings of the IEEE International Symposium on Information Theory, pp. 256–259, Austin, Texas, June 2010.
Optimal coding over the additive white Gaussian noise channel under
the peak energy constraint is studied when there is noisy feedback
over an orthogonal additive white Gaussian noise channel. As shown by
Pinsker, under the peak energy constraint, the best error exponent for
communicating an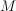 
-ary message, 
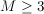, with noise-free feedback
is strictly larger than the one without feedback. This paper extends
Pinsker's result and shows that if the noise power in the feedback
link is sufficiently small, the best error exponent for communicating
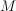an -ary message can be strictly larger than the one without
feedback. The proof involves two feedback coding schemes. One is
motivated by a two-stage noisy feedback coding scheme of Burnashev and
Yamamoto for binary symmetric channels, while the other is a linear
noisy feedback coding scheme that extends Pinsker's noise-free
feedback coding scheme. When the feedback noise power 
is
sufficiently small, the linear coding scheme outperforms the two-stage
(nonlinear) coding scheme, and is asymptotically optimal as
tends to zero. By contrast, when is relatively larger, the
two-stage coding scheme performs better.