A coding theorem for a class of stationary channels with feedback
Young-Han Kim
IEEE Transactions on Information Theory, vol. 54, no. 4, pp. 1488–1499, April 2008.
Preliminary results appeared in Proceedings of IEEE International Symposium on Information Theory, pp. 1856–1860, Nice, France, June 2007.
A coding theorem is proved for a class of stationary channels with
feedback in which the output 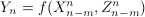 is the
function of the current and past
is the
function of the current and past 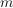 symbols from the channel input
symbols from the channel input
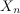 and the stationary ergodic channel noise
and the stationary ergodic channel noise 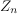 . In particular,
it is shown that the feedback capacity is equal to
. In particular,
it is shown that the feedback capacity is equal to
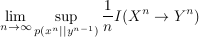
where 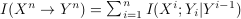 denotes the
Massey directed information from the channel input to the output, and
the supremum is taken over all causally conditioned distributions
denotes the
Massey directed information from the channel input to the output, and
the supremum is taken over all causally conditioned distributions
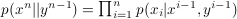 . The main
ideas of the proof are a classical application of the Shannon strategy
for coding with side information and a new elementary coding technique
for the given channel model without feedback, which is in a
sense dual to Gallager's lossy coding of stationary ergodic sources.
A similar approach gives a simple alternative proof of coding theorems
for finite state channels by Yang–Kavcic–Tatikonda, Chen–Berger,
and Permuter–Weissman–Goldsmith.
. The main
ideas of the proof are a classical application of the Shannon strategy
for coding with side information and a new elementary coding technique
for the given channel model without feedback, which is in a
sense dual to Gallager's lossy coding of stationary ergodic sources.
A similar approach gives a simple alternative proof of coding theorems
for finite state channels by Yang–Kavcic–Tatikonda, Chen–Berger,
and Permuter–Weissman–Goldsmith.