Feedback capacity of the first-order moving average Gaussian channel
Young-Han Kim
IEEE Transactions on Information Theory, vol. 52, no. 7, pp. 3063–3079, July 2006.
Preliminary results appeared in Proceedings of IEEE International Symposium on Information Theory, pp. 416–420, Adelaide, Australia, September 2005.
Despite numerous bounds and partial results, the feedback capacity of
the stationary nonwhite Gaussian additive noise channel has been open,
even for the simplest cases such as the first-order autoregressive
Gaussian channel studied by Butman, Tiernan and Schalkwijk, Wolfowitz,
Ozarow, and more recently, Yang, Kavcic, and Tatikonda. Here we
consider another simple special case of the stationary first-order
moving average additive Gaussian noise channel and find the feedback
capacity in closed form. Specifically, the channel is given by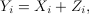 
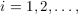where the input 
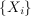satisfies a
power constraint and the noise 
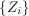is a first-order moving
average Gaussian process defined by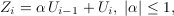 
with white Gaussian innovations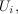 
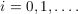
We show that the feedback capacity of this channel is
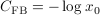
where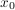 
is the unique positive root of the equation
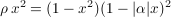
and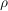 
is the ratio of the average input power per transmission
to the variance of the noise innovation 
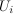. The optimal coding
scheme parallels the simple linear signaling scheme by Schalkwijk and
Kailath for the additive white Gaussian noise channel — the
transmitter sends a real-valued information-bearing signal at the
beginning of communication and subsequently refines the receiver's
knowledge by processing the feedback noise signal through a linear
stationary first-order autoregressive filter. The resulting error
probability of the maximum likelihood decoding decays
doubly-exponentially in the duration of the communication.
Refreshingly, this feedback capacity of the first-order moving average
Gaussian channel is very similar in form to the best known achievable
rate for the first-order {autoregressive} Gaussian noise channel
given by Butman.